Compounds compounds

Narrowing down the space of possibilities

To recap: I plan on testing the universality of free fall using a relatively crude experimental setup but on a very wide range of materials. This is a moderately crackpot idea, so it might work.

For sure it got mixed reactions:

Now I don’t want to get into how we (implicitly) add rules of correspondence to Peano’s axioms to reach our apparently unshakeable confidence in the fact that one plus one equals two -even though one drop of water plus one drop of water typically equals one bigger drop of water- because I would rather deal with the claim that the universality of free fall is as self evident as arithmetics.

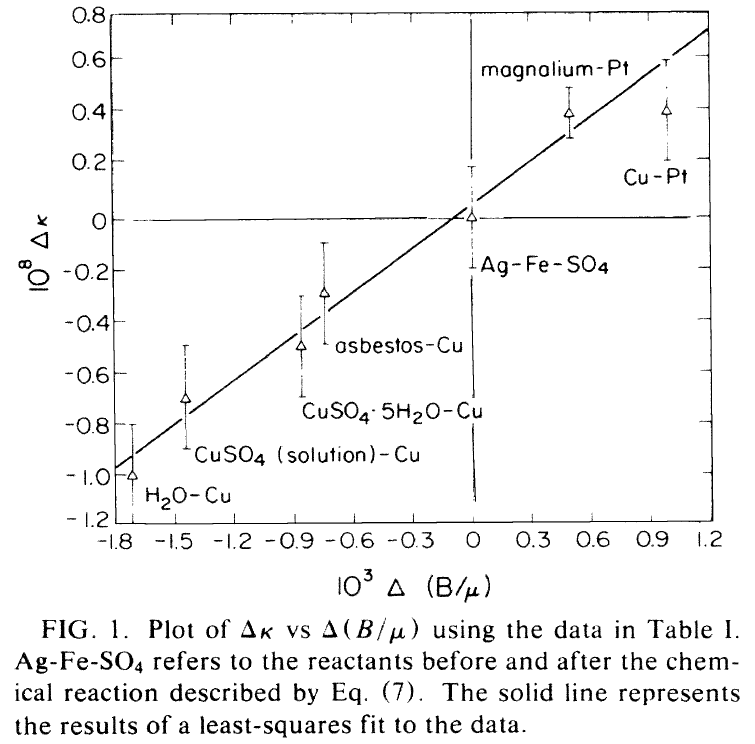
It is not. In fact Fischbach et al. 1986 reexamined the data collected by Eötvös in his first experiment (also known as the EPF experiment from the initials of the names of his coauthors) and claimed that

[the] data are sensitive to the composition of the materials used, and that their results support the existence of an intermediate-range coupling to baryon number […]

This is their Fig. 1:

showing that the difference in acceleration between any couple of materials tested by Eötvös (on the y axis) correlates with the difference in baryon number per unit mass (x axis). Also notice how most of the one-sigma error bars do not overlap with zero.

Fischbach’s paper now sits at 411 citations. I am sure that many of those question its conclusions, which are certainly not consensus today. For instance, this is a recent paper proposing a mundane explanation for the observed violation. Still, I am not aware of any controversy of this kind surrounding the empirical applicability of arithmetics, even though it happens that Peano was formulating his axioms in 1889 while Eötvös was running his experiment in 1885, making the two roughly contemporaries.

Before moving on, let’s notice that despite evidently having a thing for copper, Eötvös was still testing at least a handful of different materials, as were Potter 1923 and Bessel before him. More recent experiments seem to have considered this dimension of variation -the number of different materials tested- of secondary importance with respect to sheer precision, so that even in 2021, Fischbach writes that

It is interesting to note that since the EPF experiment, we are not aware of any experiment of comparable or greater precision that has compared the accelerations of three or more pairs of materials of different composition at the same location in the same apparatus, which would thus have been able to validate the Eotvos pattern. Some experiments, such as the floating ball experiments of Thieberger [29], or Bizzeti and Bizzeti-Sona [31], are sui generis in the sense that they would be difficult to repeat with significantly different test samples. However, the designs of some other experiments could in principle allow for direct comparisons of the accelerations of different pairs of materials. This would include the free-fall experiments of Niebauer, et al. [8], Cavasinni, et. al. [9], Kuroda and Mio [32], as well as the torsion balance experiments of the Eot-Wash collaboration [7].

So without further ado, here is my tentative list of compounds. They are 76 at present.

How did I arrive at this list? The first consideration is safety, so I included mostly compounds that score 0 or 1 in their NFPA health hazard rating and only occasionally something that scores 2 such as copper sulphate. My kids were recently playing with it trying to grow nice blue crystals, so I figured it’s safe enough.

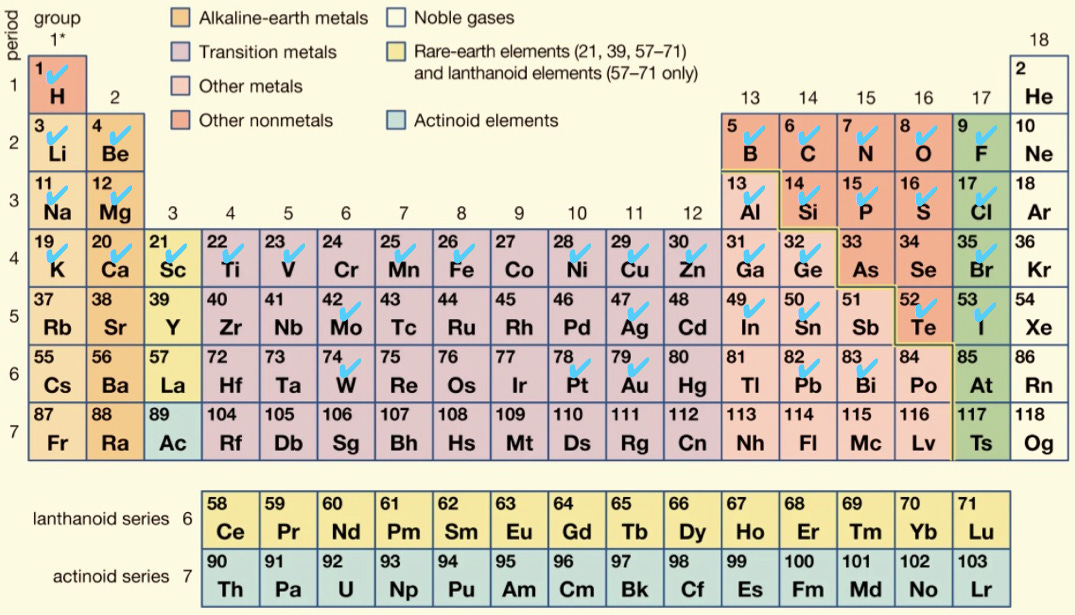
The second consideration is that I want to cover as much of the periodic table as possible. This is how I fared for now:

Basically I won’t be testing noble gases (even though maybe we could use cartridges of compressed gas for them), and after the first four periods the coverage grows spotty. Stuff begins to be radioactive or too expensive, or both. Beryllium was also a troublemaker: it seems that most of its compounds are toxic, so I settled on using aquamarine, the semi-precious stone, containing about 5% Beryllium in mass. It can be found for relatively cheap if one settles for the raw stone: apparently it’s the cutting process that makes gem-grade stuff so expensive.

Anyway, that’s about it for now, comments are welcome, as usual.