Weibull initial mass function

Just some random musings enabled by ChatGPT

The Initial Mass Function (IMF) is a sort of Holy Grail of galactic evolution and stellar physics: everyone would like to know it, but no one really does.

A mass function is, at the core, a way to describe the distribution of stellar masses in a given place. Think of a histogram. It is relatively easy -though model dependent- to measure the masses of stars in the field or in a star cluster, with the limitation that you don’t really see all the stars that are there, completeness and all that. But the initial mass function is a different beast: it’s the mass function at the time the object you are looking at was born, the mass function of the stars at birth. It’s like with people: your friend may weigh 180 pounds now but what was her weight at birth? How do you know? Stars lose mass rather than gaining it, most of the time, and it’s the opposite as with babies: it’s the ones that are too big that don’t survive long enough for us to observe them now. But you get the idea.

Typically astronomers assume that the initial mass function is a broken power law, that is a broken line in a log-log plot of frequency versus mass. As far as I know this is a choice borne out of simplicity, without a strong theoretical underpinning, though I may be wrong -I am not a stellar obstetrician. A famous initial mass function is the Kroupa IMF but there are others. All look quite empirical.

It’s been a few years now that it occurred to me that maybe a Weibull distribution would do a good job fitting the mass distribution of newborn stars. Star masses are determined by the physics driving the fragmentation of molecular clouds -lumps of cold dense gas- which in turn is driven by radiative cooling. The Weibull distribution is successfully used to describe the size distribution generated by the comminution of rocks -again, an iterative fragmentation process- see e.g. here.

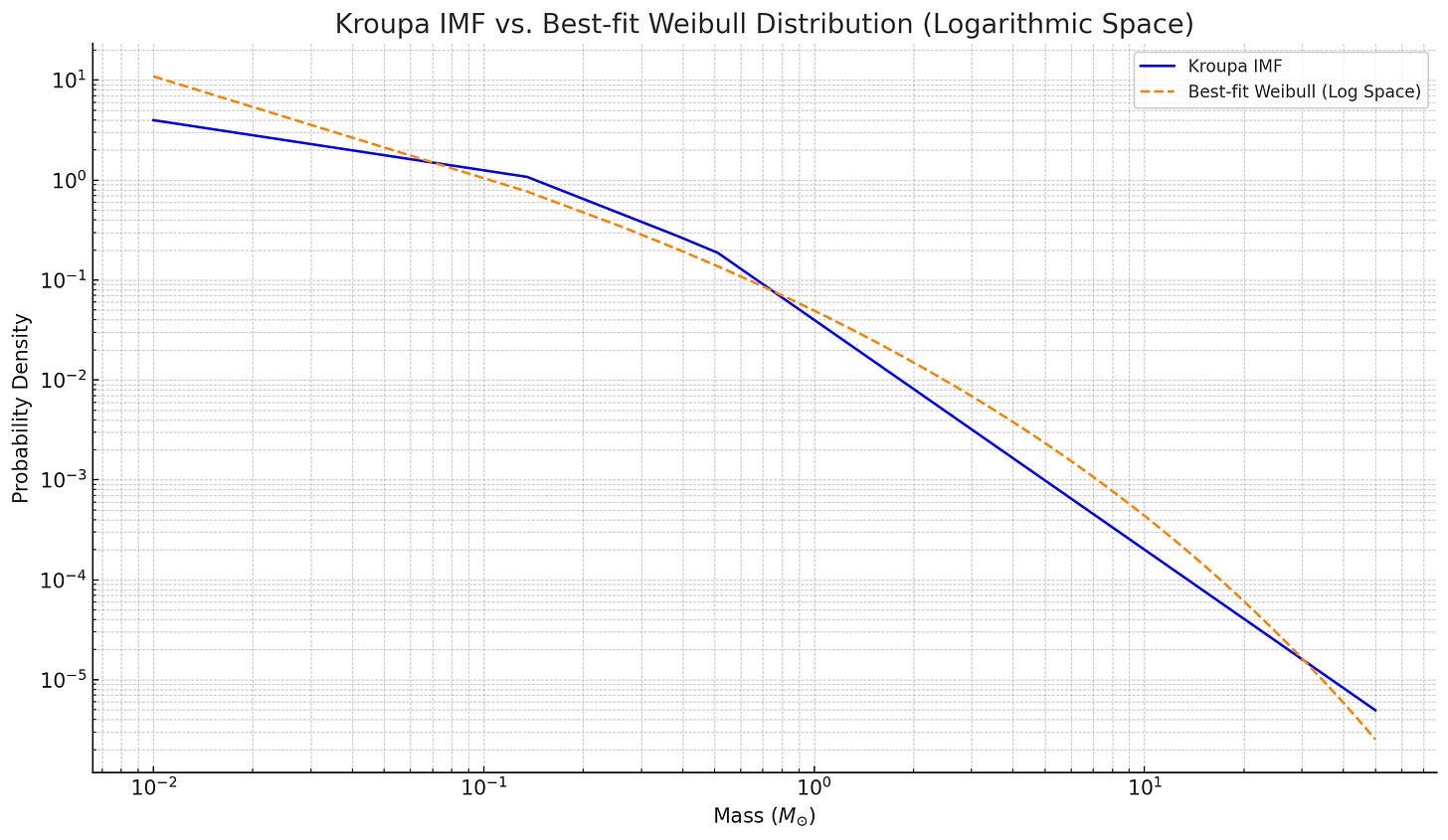
Let’s plot the Kroupa mass function together with the best fit Weibull distribution. There we go. Thanks ChatGPT advanced data analysis.

This looks like a pretty decent fit, right? It falls off quicker than a power law at high masses though, and this should have testable implications for black holes; the other side -at low masses- maybe not so much, since it’s hard to observe brown dwarves.

A final interesting point is that if you throw points uniformly at random in 3D and cluster them using agglomerative clustering with Ward’s linkage -which is probably the only reasonable way to do agglomerative clustering- the cluster sizes end up having a Weibull distribution. At some level this is again a way to model a fragmentation process (think of the randomly distributed points as gas particles deciding where to fall).