Norton's dome

How to catch something with very slippery hands

Friction lets you catch things, that is bring a moving body to rest in a finite time. Physically, friction is harder to explain that one would imagine. To make it possible, you need at a minimum an environment with a large number of degrees of freedom, more than you usually care to model. That this should be the case is clear if we look at the time reversal of catching things, that is throwing them.

Initiating movement is the classic example of free will: you choose exactly when to act. This cannot be a simple process in a deterministic world, so its time reverse cannot be either. If (the illusion of) free will has to be an emergent property in a clockwork universe, so must friction.

But, as it turns out, bringing a body to rest in a finite time is possible even in classical mechanics with no dissipation, provided your definition of classical mechanics is inclusive enough. Hence, in time-reverse, it’s possible for a body to be set in motion at an arbitrary time. This is the big deal with Norton’s dome. Granted, it will be dismissed as little more than a hack by most physicists, but perhaps it can reveal something about the implicit physical assumptions contained in the mathematics of the continuum.

Norton’s dome, Fig. 1a reproduced from Norton 2003 under fair use. Here the square-root central force is justified as the component of gravity along a suitably shaped surface.

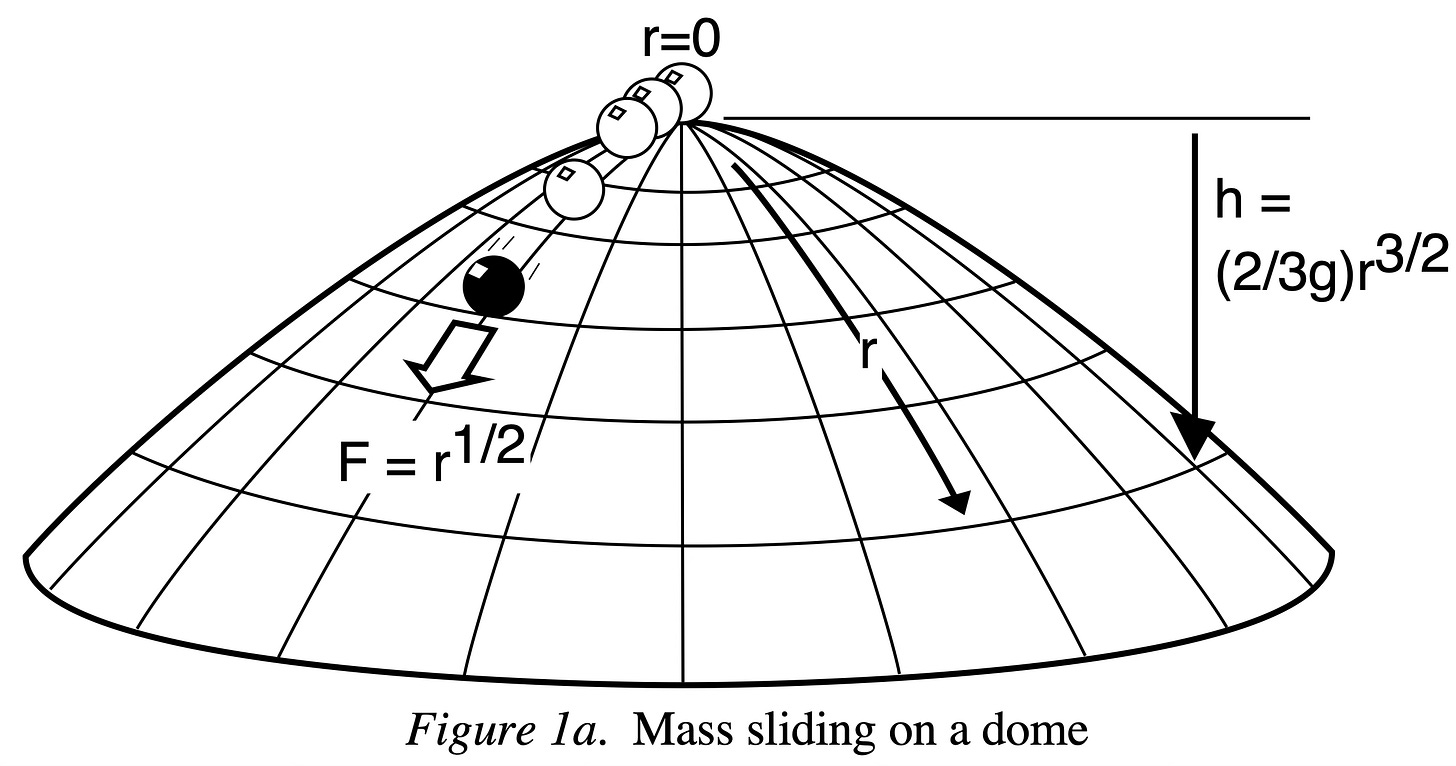
Basically, consider a central force in the form

\(F = b \sqrt{r} \)

and solve F = ma for a body that starts at rest in the origin. We get

\(m \ddot{r} = b \sqrt{r}\)

which can be solved by

\(r(t) = \frac{R}{144} (t - T)^4\)

with

\(R = \frac{b^2}{m^2}\)

Note that T is an arbitrary constant with dimensions of time. Unless I am making a stupid mistake, this solution should hold for any t, whether greater or smaller than T. Similarly, the solution r = 0 identically is good for every t. These two solutions touch at t = T (corresponding to r = 0) because the square root of r is not Lipschitz there, allowing for a lack of uniqueness.

Norton is grafting the quartic solution for t > T onto the constant one for t <= T and arguing that the resulting solution is indeterministic because motion can start after an arbitrary long wait (from minus infinity to T) at the origin. Doing this leads to a discontinuity in the fourth derivative at t = T (where it jumps from 0 to R/6) which is not present in either solution taken independently. The question then becomes whether you are allowed to do this in Newtonian mechanics, for which we need both a definition of “this” (having pathological force laws that yield non-unique solutions to an initial value problem? accepting solutions with higher-order derivatives that are discontinuous?) and of course of “Newtonian”, given that Newton’s work pre-dates modern calculus.

Before moving on, note that both the static and the full quartic solution look decidedly unproblematic. The static one obviously so, the quartic because it merely describes the motion of a body that comes in from infinity and leaves again, with the time T being singled out just by our choice of coordinates: we can set T = 0 by changing the origin of time and nothing qualitatively surprising happens at that point in time. Also both solutions are symmetric under time reversal, which Norton’s grafted solution is not. The grafting is clearly doing some heavy lifting here.

At any rate, what counts as Newtonian mechanics, and is Norton’s solution within its bounds? We all remember the three laws of motion from introductory physics courses. Here is the first one as found on nasa.gov, so it is probably good enough for rocket scientists:

An object at rest remains at rest, and an object in motion remains in motion at constant speed and in a straight line unless acted on by an unbalanced force.

that’s an almost word-for-word translation of what we read in the Principia:

Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare

This immediately gets every inquisitive student scratching their heads: is this redundant with the second law, F=ma? Why is rest treated as qualitatively different from motion, given that a change of reference frame can turn one into the other?

Typically the first question is answered in the negative: you should use the first law as (part of the) definition of inertial frame, so that you can confidently apply the second law in that frame. The second issue appears throughout in the Principia, because Newton was always making a distinction between true motion -with respect to an absolute standard of rest- and relative motion. Three pages before the introduction of the laws of motion we read

Motus verus nec generatur nec mutatur nisi per vires in ipsum corpus motum impressas

that is

True motion is neither generated nor altered unless by impressed forces acting on the moving body itself

so there is in Newton’s writing a clear distinction between creating new motion and changing existing motion, paralleling the qualitative distinction between true rest and true motion. This has been abandoned by contemporary physicists, who largely embrace Galilean relativity.

Interestingly though, this clunky formulation of the first law is more general than merely asserting that in the absence of forces a body is unaccelerated: it rules out all motion except uniform motion, which is explicitly allowed. The full quartic solution of Norton’s dome thus violates the first law in that there is a point in time (t = T) where the force is exactly zero (making the acceleration also zero) but there is non-uniform motion: the fourth derivative of position is not zero. True motion is being generated.

Norton’s grafted solution seems to me to avoid this issue because the body stays at rest up until t = T, included. Afterwards both a non-zero force and non-zero derivatives of position suddenly appear. True motion is generated not at t=T but at the first instant in which t > T.

Except that instant does not exist: the interval ]T, infinity[ is open! In Norton’s own words

We are tempted to think of the instant t = T as the first instant at which the mass moves. But that is not so. It is the last instant at which the mass does not move. There is no first instant at which the mass moves. The mass moves during the interval t > T only and this time interval has no first instant. (Any candidate first instant in t>T, say t=T+ε for any ε>0, will be preceded by an earlier one, t=T+ε/2, still in t>T.) So there is no first instant of motion and thus no first instant at which to seek the initiating cause.

Once more it looks like the prime mover (and free will and all that juicy stuff) is hiding in the last digits of the reals. There’s plenty of space there.